La Magnitudo Locale Ml (Magnitudo Richter)
La Magnitudo di Volume “body-wave” mb
La Magnitudo Superficiale Ms
La Magnitudo Durata Md
La Magnitudo Momento Mw


La magnitudo locale venne definita da Charles Richter nel 1935 a seguito dell’esigenza di realizzare il catalogo dei terremoti della California. Il problema era quello di assegnare un valore alla forza del terremoto che superasse la semplice descrizione qualitativa allora in vigore (fortissimo, forte, etc..)
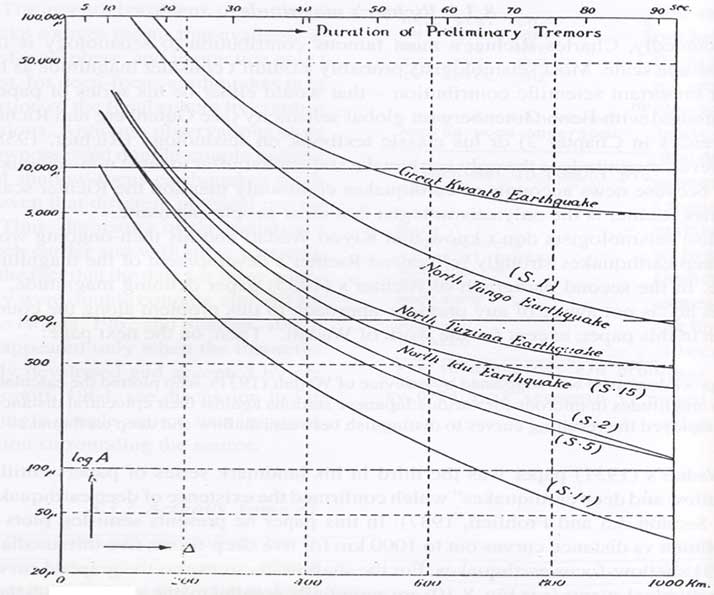
È comunemente accettata la circostanza secondo la quale la costruzione di un plot semilogaritmico, tra l’ampiezza massima registrata da un sismografo e la distanza epicentrale, in funzione di diverse classi di terremoti californiani suggerisse a Richter l’idea di una “legge di scala” della forza di un evento sismico.
 
 

Ciò che è meno noto è che tale relazione era stata già osservata dal sismologo giapponese K. Wadati nel 1931. In un suo lavoro sullo studio dei terremoti crostali e profondi riportava la figura sottostante.
Per stessa ammissione di Richter tale lavoro suggerì lo sviluppo della relazione che porta il suo nome.

La magnitudo locale è una legge empirica strumentale.
La sua definizione è:
Ml=Logaritmo in base 10 della massima ampiezza (misurata in micron) registrata da un sismografo standard a una distanza di 100 km dall’epicentro.
Lo strumento standard citato è il sismografo a torsione Wood-Anderson. Si tratta di uno strumento la cui risposta è proporzionale allo spostamento del terreno, a sole componenti orizzontali (amplificazione=2800, periodo proprio 0.8 secondi).

Si noti come proprio il carattere empirico della relazione permetta a Richter di fissare lo zero della scala. Ml=0 per un terremoto di massima ampiezza pari ad 1 micron (a 100 km di distanza). La necessità di estendere la validità della relazione a diverse distanze epicentrali impose un fattore correttivo alla formula.

Ml = log₁₀ A-log₁₀ A₀(∆)

È significativo ricordare che, come scrisse lo stesso Richter, “I did the work to provide a purely instrumental scale for rough separation of large, medium, and small shocks”…“the local magnitude scale cannot hold to any high accurracy”

Richter, ben conscio che la misura strumentale dei terremoti era fortemente condizionata dal tipo di strumento, dal tipo di onda, dalla banda di frequenza, dalla profondità dell’evento, etc, pose un “filtro” piuttosto restrittivo all’uso della relazione.

- La validità della formula è confinata entro la distanza epicentrale di 600 km. In effetti la tabella dei fattori correttivi è formulata esclusivamente entro questa distanza. Ciò per far sì che l’ampiezza massima del segnale venisse identificata nel pacchetto d’onda Lg.

- Vengono considerati esclusivamente i terremoti con profondità crostale.

- La relazione è definita in modo stringente per i terremoti caratteristici della California del Sud.
L’estensione ad altre regioni o domini tettonici deve prevedere una riformulazione del coefficiente di attenuazione.

- La magnitudo locale viene misurata attraverso la risposta all’input sismico di un sismometro a corto periodo.

- La Ml, tra le varie definizioni di magnitudo, è quella che presenta il fenomeno della saturazione a partire da valori di magnitudo più bassi (~ 6.5) rispetto alle altre scale.

A dispetto delle limitazioni prima accennate, la magnitudo locale assume ancora oggi un ruolo fondamentale. I motivi possono essere così riassunti:
- La misura della magnitudo Richter risulta assai semplice. Non richiede analisi numerica della forma d’onda.

- È stata la prima misura strumentale e perciò la più largamente usata ed è quella che permette un rapido confronto dei dati odierni con quelli registrati negli anni passati.

- La circostanza secondo la quale la Ml viene calcolata attraverso uno strumento a corto periodo (0.8 s), la rende particolarmente adatta per valutazioni attinenti all’ingegneria antisismica essendo il periodo proprio di grandi strutture vicino a tale valore.

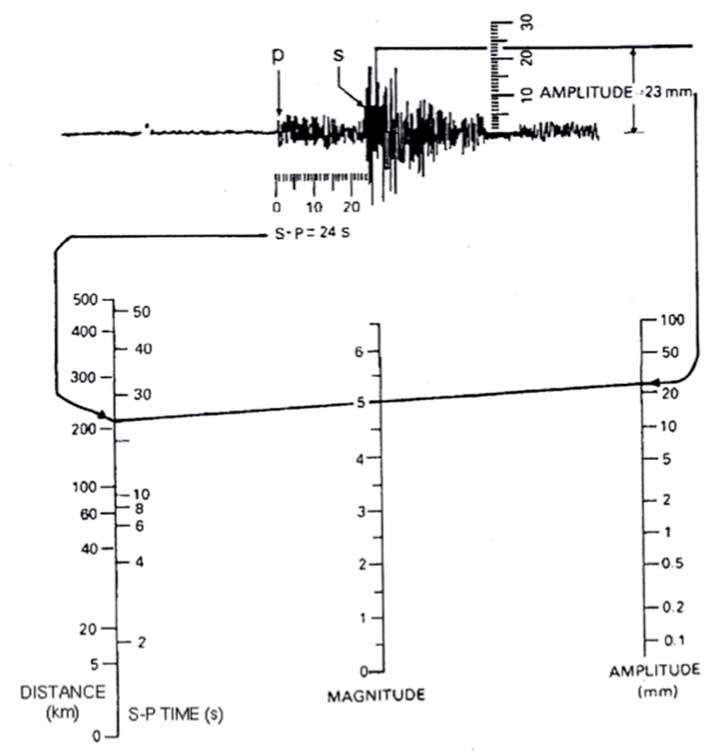
Nel corso degli anni la formula originale è stata modificata per allargarne la fruibilità e per tener conto di altri fattori come lo “spreading” della radiazione sismica e la profondità.
Le relazioni attualmente più accreditate sono 2: la relazione di Eaton (1992), utilizzata dal codice di localizzazione Hypoinverse 2000 e quella di Hutton & Boore (1987) utilizzata in IPOP.

In entrambe le formulazioni si fa riferimento all’ampiezza massima della registrazione misurata su un sismografo a spostamento Wood-Anderson. Si pone quindi il problema di determinare tale grandezza partendo dalla registrazione disponibile, che può essere stata ottenuta da un sensore anche assai diverso.

Esistono 2 metodi per ottenere la massima elongazione di un Wood-Anderson.
1 - Procedura esatta:

Essa si basa su 2 passaggi: il primo consiste nell’ottenere la registrazione del moto del terreno (se il sensore è un velocimetro si produce una integrazione del segnale),
poi si applica al segnale così ottenuto la funzione di trasferimento di un W. A. standard, calcolandone l’ampiezza massima. Il procedimento richiede il trattamento numerico di tutta la registrazione e l’applicazione di tecniche di correzione strumentale in maniera che non si producano distorsioni rilevanti nella banda di interesse, ovvero garantire che la banda passante sia sufficientemente più ampia di quella del sismometro W. A., più tecniche di filtraggio nella banda di interesse.

2) Procedura approssimata:

In questo caso non si effettua nessun trattamento del segnale per arrivare allo spostamento. Si opera direttamente sull’ampiezza massima del segnale registrato e sulla determinazione del periodo corrispondente. Si divide per la risposta strumentale in ampiezza (al periodo associato) per ottenere l’ampiezza massima in spostamento del terreno, si moltiplica poi per la risposta in ampiezza (al periodo associato) del sismometro W. A. per ottenere l’ampiezza massima del sismogramma W. A. L’approssimazione è piuttosto forte. In effetti si presuppone che il pacchetto d’onda che produce il massimo spostamento registrato sia lo stesso per i due sensori.

Il calcolo della magnitudo locale alla stazione è influenzata da fattori quali l’amplificazione locale e la “radiation pattern” dovuta alle caratteristiche geometriche della sorgente. Questa circostanza impone che il calcolo della magnitudo di un evento venga calcolata come media sul maggior numero di stazioni possibile.

La localizzazione automatica in sala sorveglianza sismica adotta la procedura esatta. Essa calcola la magnitudo locale elaborando tutta la forma d’onda delle componenti orizzontali delle stazioni digitali e applicando la media di Huber (particolarmente adatta al trattamento degli outliers)

  Esempio di localizzazione e calcolo della magnitudo locale automatica (F. Mele)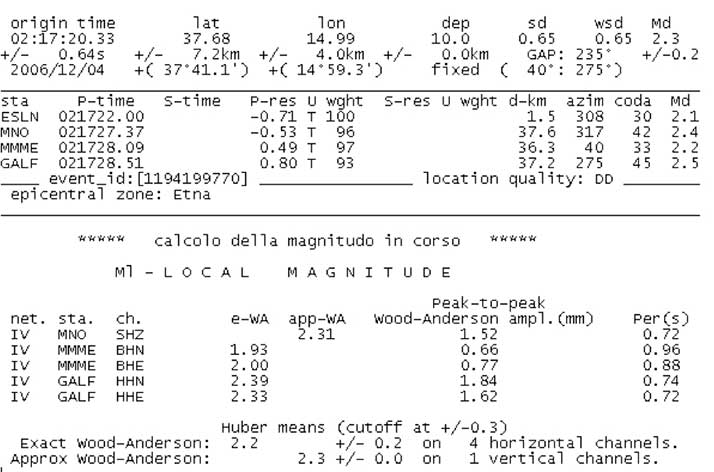

Negli anni successivi alla definizione della magnitudo locale, gli sforzi di Richter si indirizzarono al tentativo di fornire una altrettanto semplice definizione per esprimere la forza di terremoti a distanza telesismica. Il lavoro fu portato avanti insieme a B. Gutemberg per oltre 15 anni.

La grande discriminante nelle registrazioni di forti eventi telesismici riguarda la profondità.
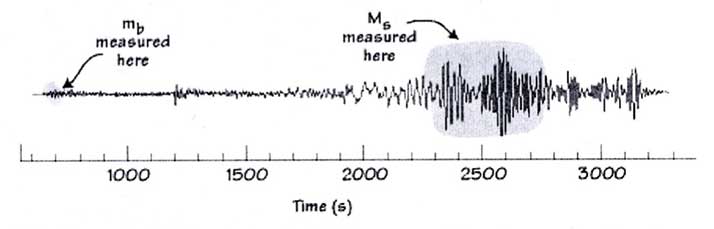
Nei forti terremoti crostali sono molto evidenti le onde superficiali, in particolare le onde di Reyleigh (comunemente note come “onde a 20 secondi”). Mentre per terremoti profondi le onde superficiali sono molto attenuate.
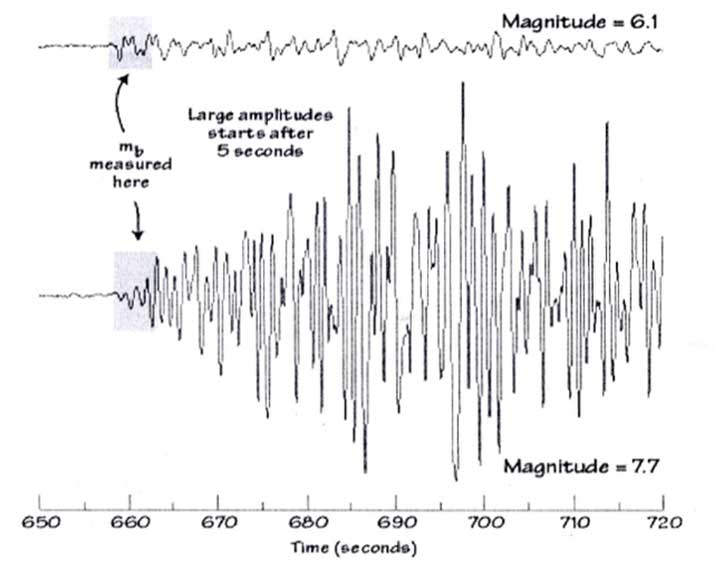
Di qui la necessità di definire due valori di magnitudo: la mb “body-wave magnitude” e la Ms

mb = log(A/T) + Q(D,h)

dove:

A = ampiezza massima in micron dello spostamento del suolo, misurata sulla componente verticale della fase P nel pacchetto associato al primo arrivo, nell’intervallo di periodo 0.1 < T < 3
T = periodo in secondi
D = distanza epicentrale in gradi
h = profondità in km
Q(D,h) = fattore correttivo empirico

La mb è definita per D > 5 ed è particolarmente utilizzata nel controllo delle esplosioni nucleari.

Ms = log(A/T) + 1.66 log(D) + 3.3

dove:

A = ampiezza massima in micron dello spostamento del suolo, misurata sulla componente verticale delle onde superficiali nell’intervallo di periodo 18 < T < 22 secondi
T = periodo in secondi
D = distanza epicentrale in gradi 

La MS è definita per 20 < D < 160 e per profondità inferiori a 50 km

La magnitudo durata Md ha come forma generale la seguente definizione:

MD = a log(Dur) + bD + ch + e

dove:

Dur = durata in secondi dall’arrivo P fino a quando il segnale in coda raggiunge il segnale di noise.
D = distanza epicentrale in km
h = profondità in km
a,b,c,e = coefficienti numerici di best-fit

Alcune formulazioni utilizzate in I.N.G.V.:
MD = 2.0 log(Dur + 0.082 D) – 0.87 Console & Di Sanza (1988)
MD = 2.49 log(Dur) – 2.31 + CORRsta Castello, Olivieri & Selvaggi (2005)

La magnitudo momento Mw è stata formulata in anni recenti da Hiroo Kanamori (1977). La sua formulazione è:

Mw = 2/3 log(M0) -10,73

Dove:

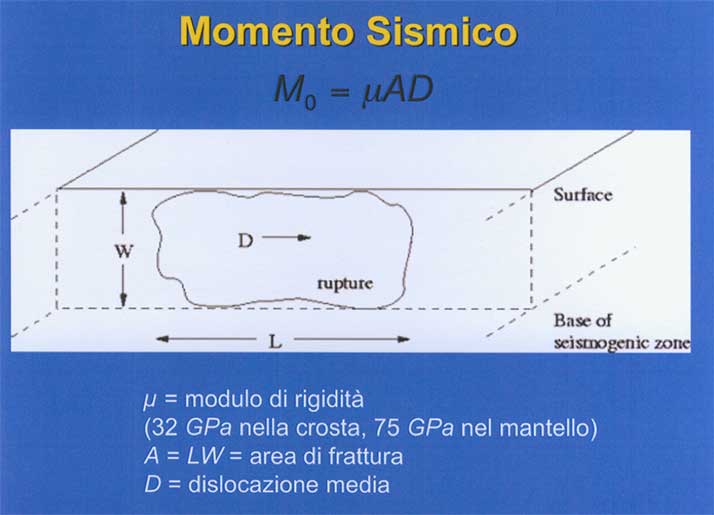
M0 = momento sismico (dyne x cm)

Grazie alle grandezze coinvolte nella sua definizione, la magnitudo momento non è affetta dal fenomeno della saturazione

Va rimarcata la circostanza secondo la quale la magnitudo momento è l’unica tra quelle presentate che abbia un chiaro significato fisico. Essa, attraverso il momento sismico, tiene conto di 2 grandezza fisiche essenziali quali l’area dello specchio di faglia e lo spostamento medio compiuto dalla stessa.
Per rendere evidente l’utilità della Mw si consideri l’esempio sottostante.